
The quantum oscillation phenomena driven by magnetic fields in condensed matter physics systems are mostly very elegant, and their emergence is related to specific physical mechanisms. For example, in the Little-Parks experiment with superconducting rings, periodic oscillations of the superconducting transition temperature (Tc) with magnetic field (B) can be observed; in mesoscopic conductor rings, Aharonov-Bohm and Altshuler-Aronov-Spivak oscillations with B as the oscillation period appear. Both of these quantum oscillations involve magnetic flux quantization. Furthermore, in the de Haas-van Alphen (dHvA) and Shubnikov-de Haas (SdH) effects, some observable physical quantities exhibit oscillations with a period of 1/B, originating from the Landau quantization of electron orbits in a magnetic field. Recently, resistance oscillations with logarithmic magnetic field have also been reported in certain systems.
Recently, a team led by Researchers Qu Fanming and Lu Li from the Q02/HX-Q02 Group of the Solid State Quantum Information and Computation Laboratory at the Institute of Physics/National Center for Condensed Matter Physics, Chinese Academy of Sciences, collaborated with Researcher Zhou Yi's team from the T06 Group, Researcher Shi Youguo's team from the HM-01 Group, and Professor Liu Fucai's team from the University of Electronic Science and Technology of China, to discover a new type of electrically driven quantum oscillation phenomenon in one-dimensional nanowires based on charge density waves (TaSe4)2I and TaS3. Specifically, the voltage V exhibits periodic oscillations with the reciprocal of current 1/I. Phenomenologically, this oscillation with a period of 1/I bears a striking resemblance to the magnetically driven quantum oscillations of dHvA and SdH with a period of 1/B.
(TaSe4)2I and TaS3 are quasi-one-dimensional charge density wave materials with van der Waals structures. The research team obtained their nanowires using the tape exfoliation method, prepared electrodes using Ti/NbTiN or Ti/Nb materials, and analyzed the changes in their voltage-current (V-I) characteristics with temperature. As the temperature decreased from room temperature through the charge density wave transition temperature TCDW to the system's base temperature of 1.55 K, the V-I curves gradually exhibited nonlinear behavior, and the differential resistance approached zero within a certain current range, indicating the emergence of an ideal Fröhlich conduction state (with the differential conductance tending to infinity). Interestingly, in the Fröhlich conduction region, V exhibited sawtooth-like oscillations with I. When the horizontal axis was converted to 1/I, periodic oscillations were observed (Figures 1, 3, 4), and the oscillation index n could reach 1 (Figure 3). This oscillation phenomenon could be reproduced in different devices and different charge density wave materials. Through measurements on a large number of devices, the research team believed that its appearance required specific conditions, including but not limited to: low dissipation at the electrode-material interface, low electromagnetic noise interference, pure charge density wave current (good insulation before slipping), and temperatures far below TCDW (Figures 2, 4).
Researcher Zhou Yi's preliminary theoretical model suggests that in a charge density wave insulator, current-driven slipping can be equivalent to the existence of a time-periodic potential, capable of generating Floquet subbands (Figure 4). With these subbands as mediators, electrons at one electrode enter the other electrode through resonant tunneling (coherent transport). Therefore, when the electrode's Fermi level aligns with a subband in the charge density wave nanowire, it corresponds to a sudden drop in voltage in the V-I curve, i.e., voltage oscillation. Under this premise, the model also cleverly gives the oscillation law with a period of 1/I, which is consistent with the experimental results.
The related research results were published in Physical Review B with the title "Inverse-current quantum electro-oscillations in a charge density wave insulator". Postdoctoral researcher Le Tian (formerly at the Q02/HX-Q02 Group) and PhD candidate Jiang Ruiyang are the co-first authors, and Researchers Qu Fanming and Lu Li are the co-corresponding authors. Collaborators also include Associate Researcher Luzhaozheng, Distinguished Researcher Shen Jie, Researcher Liu Guangtong, Associate Researcher Li Zhilin, and Professor Cao Xuewei from Nankai University. This work was supported by the National Key Research and Development Program, the National Natural Science Foundation of China, the Strategic Priority Research Program of the Chinese Academy of Sciences, the Major Project of "Quantum Communication and Quantum Computer" under the Science and Technology Innovation 2030 initiative, and the Comprehensive Extreme Conditions Experiment Facility.
Link to the related work: https://doi.org/10.1103/PhysRevB.109.245123
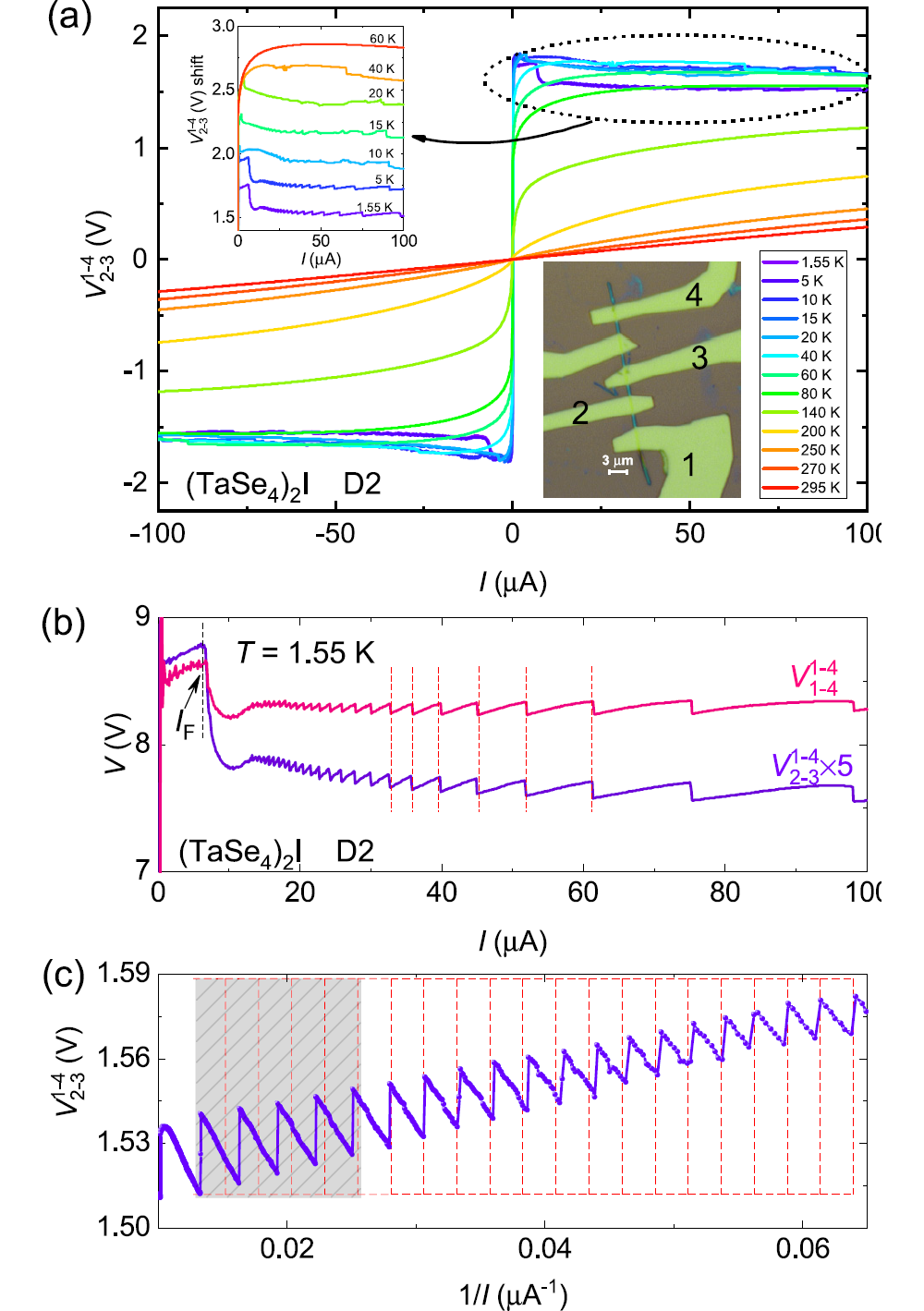
Figure 1.a. Temperature-dependent V-I curves of (TaSe4)2I nanowire device D2; b. Sawtooth-like oscillation of voltage V with current I at 1.55K; c. Voltage V as a function of the reciprocal of current 1/I.
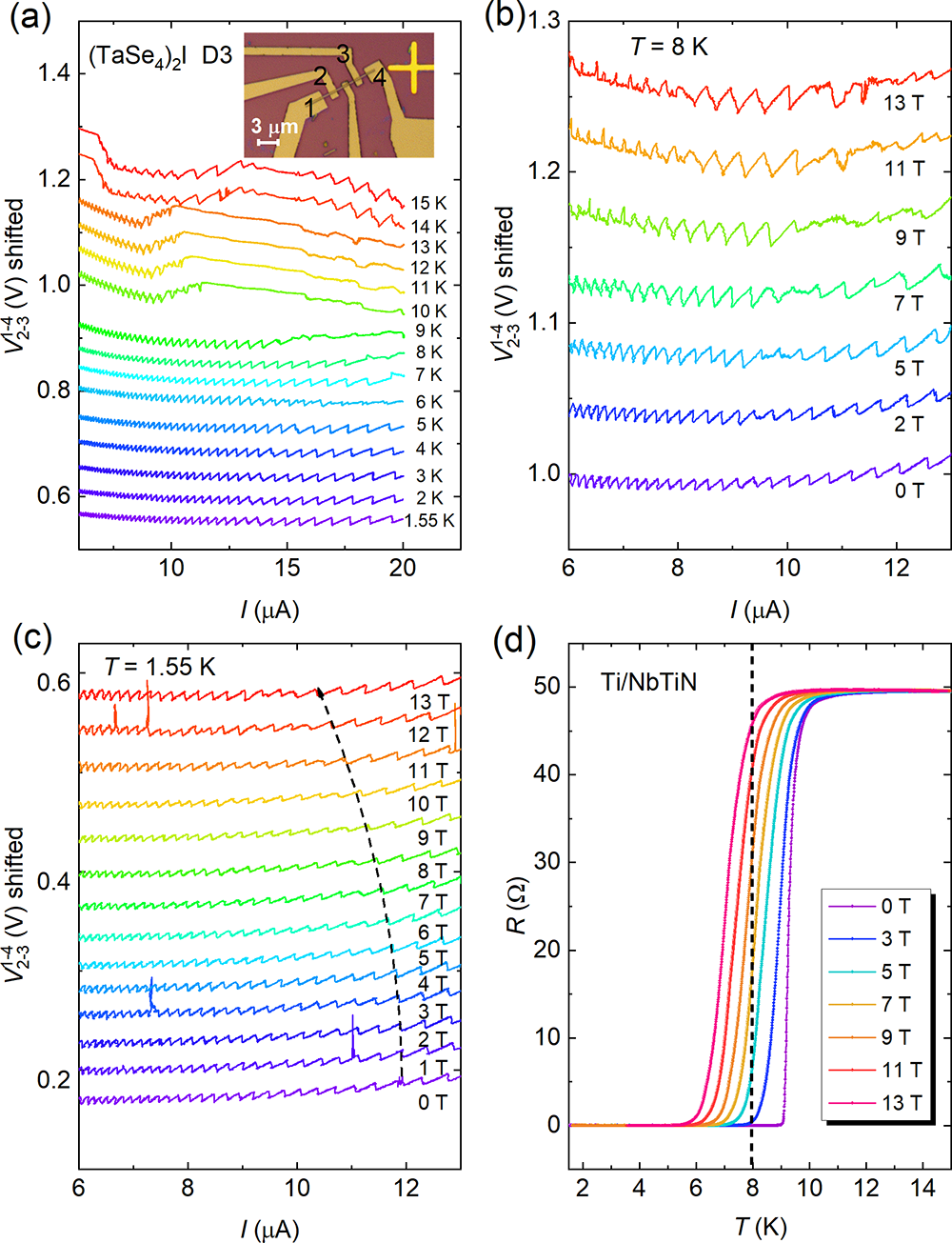
Figure 2.a. Temperature-dependent oscillation in the V-I curves of (TaSe4)2I nanowire device D3, where the oscillation becomes blurred when the temperature exceeds the superconducting transition Tc of NbTiN; b. Magnetic field-dependent oscillation in the V-I curves at 8K, where the oscillation starts to blur as the external magnetic field rises above the upper critical field Hc2 of NbTiN; c. Magnetic field-dependent oscillation in the V-I curves at 1.55K; d. R-T curves of Ti/NbTiN electrodes as a function of magnetic field.
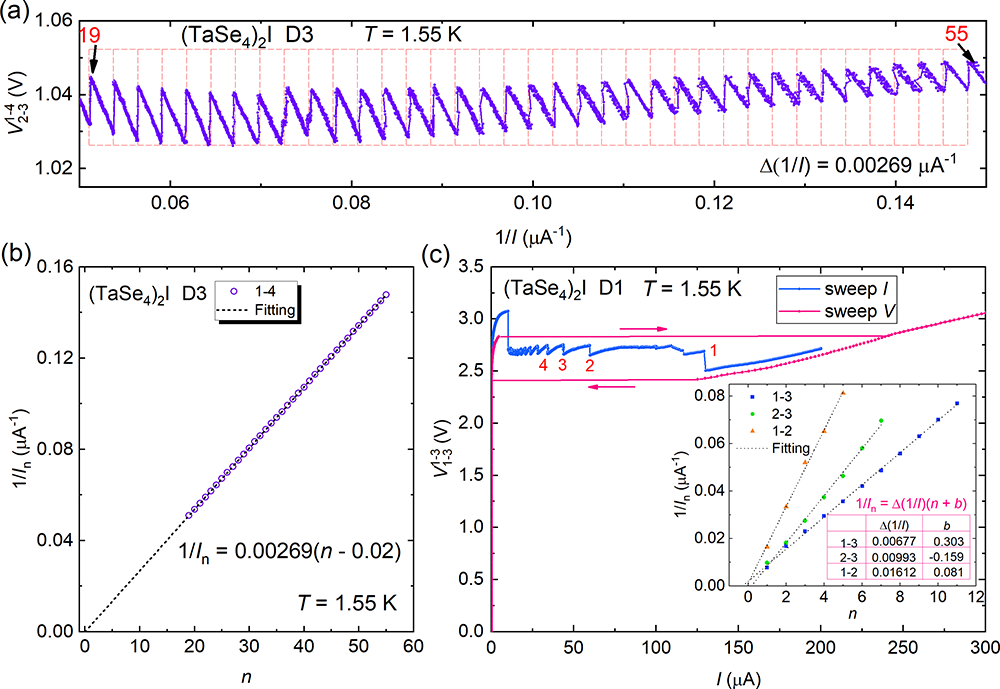
Figure 3.a. Perfect periodicity of V as a function of 1/I in (TaSe4)2I nanowire device D3; b. Linear behavior of 1/In at each oscillation position in the V-I curve of D3 as a function of oscillation index n; c. Observation in device D1 where the oscillation index n reaches 1, followed by the disappearance of oscillation with increasing current.
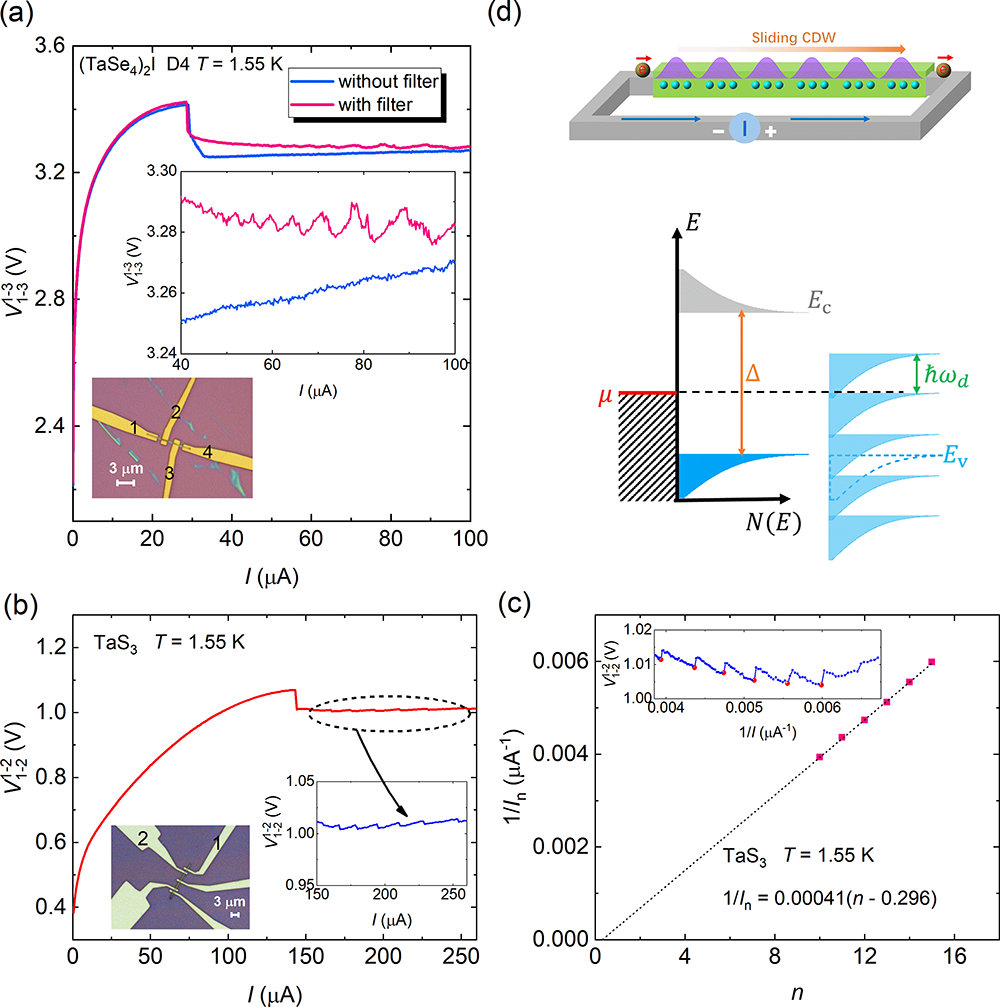
Figure 4.a. Enhanced oscillation in the measurement circuit after adding filtering; b and c. Observation of 1/I-periodic oscillation in TaS3 nanowire devices; d. Resonance tunneling model mediated by Floquet subbands in the sliding charge density wave state.